컴공댕이 공부일지
[실전 알고리즘] 0x0C강 | 백트래킹 (Backtracking) - 이론 & 예제문제 풀이 / next_permutation 함수의 활용 본문
[실전 알고리즘] 0x0C강 | 백트래킹 (Backtracking) - 이론 & 예제문제 풀이 / next_permutation 함수의 활용
은솜솜솜 2025. 4. 13. 01:03
🔎 백트래킹이란?
현재 상태에서 가능한 모든 후보군을 따라 들어가며 탐색하는 알고리즘
가능한 모든 선택지를 다 플레이해보는 것 !
이렇게만 보면 브루트포스랑 뭐가 다른가 싶은데,
브루트포스는 별도의 조건을 고려하지 않고, 단순히 모~든 조합을 싹 다 고려한다.
반면, 백트래킹은 가능한 경로만을 탐색하며,
특정 조건을 만족하지 않는 경우는 더 이상 진행하지 않고 이전으로 BACK한다.
이번 글에서는 바킹독 선생님의 강의를 기반으로, 백트래킹 연습 문제를 풀이해볼 것이다.
BFS 문제와 비슷하게, 기본적인 코드 형태만 익혀두면 응용할 부분은 잘 없는 유형이라 할 만 할거라고 ..!
📝 백트레킹 예제 (1) - N과 M (1)
백준 15649번 N과 M (1) (https://www.acmicpc.net/problem/15649)
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
#include <iostream>
using namespace std;
int n,m;
int arr[10];
int isUsed[10];
void func(int k) {
// 종료조건 - 배열에 채워진 수(k)가 m개가 되면, arr 출력 후 종료 ~
if(k==m) {
for(int i=0; i<m; i++) {
cout << arr[i] << " ";
}
cout << '\n';
return;
}
for(int i=1; i<=n; i++) {
if(!isUsed[i]) { // 아직 사용되지 않은 수라면,
arr[k] = i; // 배열에 추가하고
isUsed[i] = true; // 사용 여부 표시
func(k+1); // 재귀 호출
isUsed[i] = false; // 재귀 마친 후, i 넣기 전으로 백트래킹
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
func(0);
return 0;
}
📝 백트레킹 예제 (2) - N-Queen
백준 9663번 N-Queen (https://www.acmicpc.net/problem/9663)
- NxN 2차원 좌표에서, N개의 퀸을 놓을 수 있는 배치의 수.
첫번째 풀이 ( 이전 행에 놓여있는 퀸들을 모두 순회하며, 놓을 수 있을 지 체크 )
#include <iostream>
using namespace std;
int n, cnt = 0;
int board[16]; // 각 행에 퀸 없으면 0, 있으면 퀸이 놓인 열의 값을 저장할 배열.
bool check(int x, int y) {
for(int i=0; i<x; i++) {
if(board[i]==y || abs(i-x)==abs(board[i]-y)) return false;
}
return true;
}
void func(int cur) {
if(cur==n) { // 퀸 n개 다 놓았으니 종료.
cnt++;
return;
}
for(int i=0; i<n; i++) {
if(!check(cur, i)) continue; // 퀸을 놓을 수 없음.
board[cur] = i; // cur행 i열에 퀸 놓음.
func(cur+1); // 다음행 탐색.
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
func(0);
cout << cnt;
return 0;
}
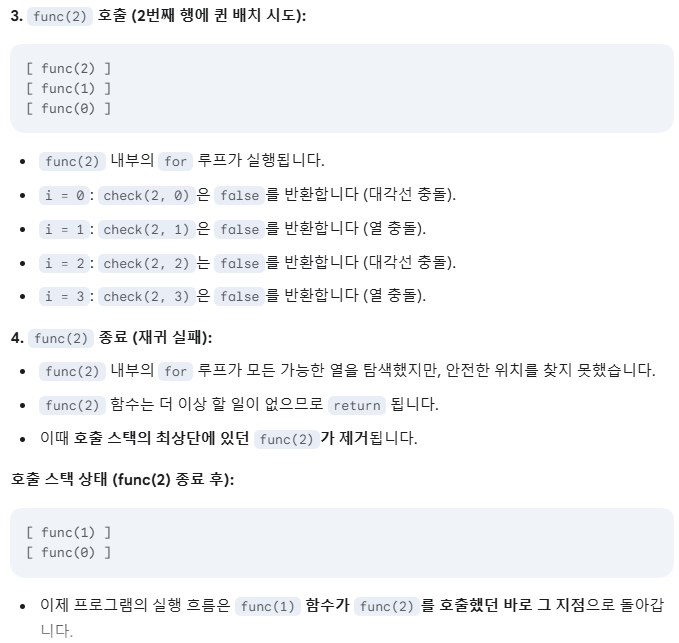
아직 재귀가 많이 낯설어서.. 어떤 부분이 back해서 돌아간다는거지..? 헷갈렸었는데 아래 사진처럼 예시를 보면 알 수 있다. func(0) → func(1) → func(2) 식으로 각 행마다 가능한 위치에 퀸을 놓아나간다. func(cur+1)을 호출 및 실행해 다음 행에 퀸을 놓을 장소를 찾고, 실패하면 아직 종료되지 않은 이전 func(cur)로 마저 돌아간다.
▼ 호출 스택에 함수가 호출되는 과정.

👀 코드 피드백 ; 시간복잡도 개선의 필요성 ㅡ isUsed 배열 활용하기
첫번째 예제였던 n과 m 문제에선, 중복없는 수열을 만들기 위해 isUsed라는 배열을 두고 해당 수가 이미 쓰였는지를 체크했다. 수열을 하나하나 순회하며 해당 수가 이미 쓰였는지 점검하는 것은 시간이 너무 걸리기 때문에(O(N)) isUsed를 통해 이미 쓰인 수를 표기해두면서 문제를 풀어나갔다. 위의 N-Queen문제도 비슷한 방식을 활용할 수 있다.
기존의 코드는 각 퀸을 놓을 때마다 이전 행들에 놓인 퀸들을 모두 점검한다. n이 크지 않아 시간 내 맞추긴 했지만 비효율적인 방법이다. isUsed를 사용하면 보다 빠르게 개선될 수 있다.
개선된 두번째 풀이 ( isUsed로 이미 놓인 열, 대각선을 표기해두기 )
#include <iostream>
using namespace std;
int n, cnt = 0;
bool isUsed0[15]; // 각 열의 중복 체크할 배열
bool isUsed1[30]; // 우상향 대각선의 중복 체크할 배열 : x+y
bool isUsed2[30]; // 우하향 대각선의 중복 체크할 배열 : x-y+(n-1)
void func(int x) {
if(x==n) { // 퀸 n개 다 놓았으니 종료.
cnt++;
return;
}
for(int y=0; y<n; y++) {
if( !isUsed0[y] && !isUsed1[x+y] && !isUsed2[x-y+n-1] ) {
isUsed0[y] = true;
isUsed1[x+y] = true;
isUsed2[x-y+n-1] = true;
func(x+1);
isUsed0[y] = false;
isUsed1[x+y] = false;
isUsed2[x-y+n-1] = false;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
func(0);
cout << cnt;
return 0;
}
위와 같이 isUsed로 특정 열과 대각선에 이미 퀸이 놓여있는 지를 boolean 배열로써 표기하면, 이전의 풀이처럼 매번 반복문을 돌며 이전의 퀸들을 일일이 체크하지 않으니 빠르다.

+ 시간복잡도 . . .
이 문제에서 우리는 시간복잡도를 제대로 파악하기가 많이 힘듭니다. 열만 가지고 생각을 해보면 O(N!)이니 N = 14일 때 조금 애매한데 실제로 구현을 해서 돌려보면 꽤 빠르게 돕니다.
A1에 퀸을 놓으면 바로 B1, B2에 퀸을 놓는 경우는 해볼 필요가 없어지는 것과 같은 상황을 백트래킹에서 가지치기라고 부르는데 가지치기가 빈번하면 백트래킹의 시간복잡도를 가늠하기가 많이 힘듭니다. 그렇기 때문에 문제를 보고 시간복잡도가 가늠이 잘 안가는데 N이 많이 작아 백트래킹으로 푸는 문제일 것 같다는 생각이 들면 직접 구현한 뒤 가장 시간이 오래 걸릴만한 케이스를 직접 돌려봐서 시간 초과가 나는지 안나는지를 보면 됩니다. 이 문제라면 N = 14를 넣어보는 것입니다. 만약 시간이 애매하면 최대한 최적화할 수 있는 것들을 찾아서 고치고 제출을 하면 됩니다. 시간을 로컬에서 측정할 때에는 반드시 Release 모드로 실행을 해야 하고 보통은 서버가 로컬보다 빠르다는 점도 기억하시면 좋습니다. Release 모드가 무엇인지는 구글에 한 번 검색해보세요.
📝 백트레킹 예제 (3) - 부분수열의 합
백준 1182번 부분수열의 합 (https://www.acmicpc.net/problem/1182)
- 합이 S가 되는 부분 수열 개수 구하는 문제
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, s, cnt;
bool flag;
int arr[30];
bool isUsed[30];
void func(int x, int sum) {
if(x == n) { // 배열 다 돌았거나,
if(sum==s) cnt++; // 합이 s와 같을 때 종료.
return;
}
// 해당 수를 더한 경우.
func(x+1, sum+arr[x]);
// 해당 수를 더하지 않은 경우.
func(x+1, sum);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> s;
for(int i=0; i<n; i++) {
cin >> arr[i];
}
func(0, 0);
if(s==0) cnt--; // 아무것도 선택되지 않은 경우 제외.
cout << cnt;
return 0;
}
주어진 n개의 배열을 모두 돌았거나, 골라둔 부분 수열의 합이 s와 같은 경우 조건을 달성했으니 종료해준다. 그리고 해당 숫자를 선택한 경우, 아닌 경우 각각 재귀 호출을 한다. 위의 문제들은 반복문으로 배열을 순회하며 특정 조건이 맞는 수를 채택하는 방식이라면, 이 문제는 전체 배열을 돌면서 넣을지 말지 각각 분기한다. 형태도 다르고 재귀 구조도 인자 2개로 살짝 달라서.. 어려웠당 .... 한참 고민해도 모르겠어서... ㅎ 힌트 보고 풀엇음 ㅠㅅㅠ 재귀진쨔어려워 !!!!
👍 순열과 조합이 필요할 때 - STL next_permutation
순열과 조합이 문제에 필요한 경우, 무조건 next_permutation 함수를 사용할 것 !
✳️ next_permutation
C++ STL에서 제공하는 함수로, 주어진 순열의 다음 순열을 계산. (알고리즘 헤더)
사전순으로 다음 순열을 배열해주는 함수 ! 다음 수열이 존재하지 않는다면 false
- 순열(순서 O) 만들기 → 3 이하의 자연수를 순서있게 뽑는 경우
int a[3] = {1, 2, 3};
do{
for(int i=0; i<3; i++)
cout << a[i];
cout << '\n';
}while(next_permutation(a, a+3));
/*
123
132
213
231
312
321
*/
- 조합(순서 X) 만들기 → 4 이하의 자연수 중, 2개를 순서없이 뽑는 경우
int a[4] = {0, 0, 1, 1};
do{
for(int i=0; i<4; i++) {
cout << a[i];
} cout << '\n';
}while(next_permutation(a, a+4));
/*
0011
0101
0110
1001
1010
1100
*/
int a[4] = {0, 0, 1, 1};
do{
for(int i=0; i<4; i++) {
if(a[i]==0) cout << i+1;
} cout << '\n';
}while(next_permutation(a, a+4));
/*
12
13
14
23
24
34
*/
n과 m 시리즈 다 풀어보고, next_permutation 사용한 방식으로도 풀어보라구 하시네요 :).. 이야 풀 문제 많다 하하...
아직 완벽히 숙지되지 않은 것 같으니.. 문제 열심히 풀면서 익혀봐야겠다. 암튼 일단 백트래킹도 강의 내용 정리 완료 ! 😵
[실전 알고리즘] 0x0C강 - 백트래킹
이번에는 백트래킹을 배워보도록 하겠습니다. 백트래킹도 재귀와 더불어 많은 사람들이 고통을 호소하는 알고리즘 중 하나이지만 의외로 그 재귀적인 구조에 매료되어서 참재미를 알아버리는
blog.encrypted.gg
'PS > 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x0B강 | 재귀 (Recursion) - 이론부터 예제 문제풀이까지, 재귀 문제의 구조 완벽 익히기 😎 (5) | 2025.03.21 |
|---|---|
| [실전 알고리즘] 0x0A강 | 깊이 우선 탐색 (DFS) - 스택으로 DFS 구현하기 / DFS와 BFS의 차이? (0) | 2025.02.13 |
| [실전 알고리즘] 0x09강 | 너비 우선 탐색 (BFS) - 응용 문제 유형별로 풀어보기 📝 (0) | 2025.02.13 |
| [실전 알고리즘] 0x01강 - 🔎 정수 및 실수 자료형의 특징 / 2의 보수법 (0) | 2025.01.15 |
| [ 동적계획법 ] top-down, bottom up (상담시간 퇴사 문제) (0) | 2024.04.02 |




